Ce sujet est en construction

Bonjour,

Oulalah, quel titre barbare ! Vous vous posez sans doute une flopée de questions existentielles, venues à votre esprit sous l'impulsion de cette phrase grotesque.

Cet article aura pour but de synthétiser la démonstration d'un fait remarquable : Pourquoi la surface libre de l'eau d'un verre - ou tout autre récipient à géométrie cylindrique - se creuse-t-elle lorsqu'on l'agite circulairement (avec une cuillère ou d'un coup de poignet) ?

Déjà, qu'est-ce que la surface libre ?

Si nous considérons le milieu liquide, nous pouvons l'isoler par la pensée comme un volume délimité par une surface. Cette surface coïncide pour une partie avec la forme du récipient. Il s'agit d'une contrainte spatiale.

Une partie, cependant, reste à l'air libre ou en contact avec un autre gaz. Sa forme est imposée par des contraintes de pression et de tension surfacique, au niveau de la séparation des phases : C'est la surface libre.

"Ah oui", me direz-vous, "cela me fait penser à l'essoreuse qui, quand on la met en rotation, plaque les feuilles de salade contre la paroi latérale !"

Ce à quoi je répondrai "Presque !" même si, dans l'immédiat, il s'agit du même phénomène qui entre en jeu. La différence, elle, réside dans le fait que nous parlons de mécanique du solide dans le cas de la salade, et de mécanique des milieux continus en parlant d'eau.

Mais pourquoi pas expliquer ce qui se passe dans le cas de la salade :

1) Accélération d'entraînement, dite accélération centripète dans le cas d'un mouvement de rotation uniforme

L'accélération est définie en mécanique classique comme étant l'évolution de la vitesse qui, elle, est l'évolution continue de la position du solide dans le temps. Pour faire très bref, si l'accélération est positive (dans un repère galiléen donné), la vitesse augmente. Si elle est négative, la vitesse diminue. Et si elle est nulle, la vitesse ne change pas.

Dans le cas d'un mouvement circulaire, nous observons systématiquement une accélération et ce même si la vitesse du solide (vitesse orthoradiale) ne change pas en norme (en valeur). Ce genre de mouvements est dit de "rotation uniforme" :

On observe la vitesse en vert, désignée par un vecteur de norme (représentée par la longueur de la flèche) constante.

Cette accélération est dirigée vers le centre, et en voici une démonstration mathématique :

Tout mouvement dans un système à symétrie cylindrique peut être paramétré dans un repère de Frenet (base de Frenet + horloge), constitué de deux vecteurs orthogonaux de norme unitaire (valant 1), pouvant tourner au fil du mouvement. Nous nommerons ces deux vecteurs le vecteur radial [TEX]\vec{e_r}[/TEX] et le vecteur orthoradial, [TEX]\vec{e_{\theta}}[/TEX]. Noter que la vitesse, ci-dessus, est orthoradiale, car dirigée dans la direction orthogonale directe vis-à-vis du rayon.

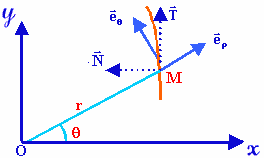
Base de Frenet associée à un point mobile M. On peut aussi lire sur ce schéma la base de vecteurs [TEX](\vec{N},\vec{T})[/TEX] qui est associée au plan cartésien et qui, elle, ne peut pas tourner au gré du mouvement de M.

La position d'un point donné, dans la base de Frenet, est donnée par le vecteur [TEX]\vec{r} = r\vec{e_r} + z\vec{e_z}[/TEX]

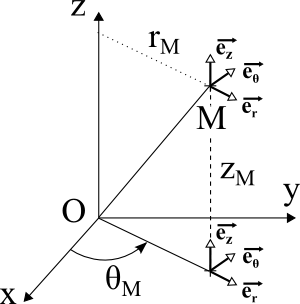
Pour trouver la vitesse, nous dérivons par rapport au temps, ce qui donne :

[TEX]\vec{v} = \frac{\mathrm{d}\vec{r}_{\ \mathcal{R}}}{\mathrm{d}t} = \dot{r}\vec{e_r} + r\frac{\mathrm{d}\vec{e_r}_{\ \mathcal{R}}}{\mathrm{d}t} = \dot{r}\vec{e_r} + r\dot{\theta}e_{\theta}[/TEX] puisque [TEX]\frac{\mathrm{d}\vec{e_r}_{\ \mathcal{R}}}{\mathrm{d}t} = \frac{\mathrm{d}\vec{e_r}_{\ \mathcal{R}}}{\mathrm{d}\theta} \frac{ \mathrm{d}\theta}{\mathrm{d}t} = \vec{e_{\theta}}\dot{\theta}[/TEX]

En redérivant par rapport au temps, nous trouvons l'accélération : [TEX]

\vec{a} = \frac{\mathrm{d^2}\vec{r}_{\ \mathcal{R}}}{\mathrm{d}t^2} = \(\ddot{r}-r\dot{\theta}^2\)\vec{e_r} + \(2\dot{r}\dot{\theta} + r\ddot{\theta}\)\vec{e_{\theta}} + \ddot{z}\vec{e_z}[/TEX].

Remarquons maintenant que si le mouvement est un mouvement circulaire uniforme, le rayon du mouvement ne varie pas, ce qui permet d'ignorer tout terme en [TEX]\dot{r}[/TEX] ou en [TEX]\ddot{r}[/TEX]. La vitesse orthoradiale ne varie pas tout court, ce qui permet d'ignorer le terme en [TEX]\vec{e_{\theta}}[/TEX], et la position axiale non plus ne varie pas. Cela nous laisse au final :

[TEX]

\vec{a} = -r\dot{\theta}^2\vec{e_r} = \vec{a}_{\mathrm{centripete}}[/TEX] : L'accélération est centripète, dirigée vers le centre du mouvement. On peut la lire, en rouge, dans le premier schéma.

2) Force d'inertie

La force d'inertie [TEX]\vec{F}_{in}[/TEX] s'appliquant à un objet en mouvement non rectiligne uniforme est directement liée à l'accélération d'entrainement via la relation :

[TEX]\vec{F}_{in} = -m\vec{a}_{\mathrm{entrainement}}[/TEX] où m est la masse de l'objet.

On a donc dans le cadre du mouvement circulaire uniforme :

[TEX]\vec{F}_{in} = -m\vec{a}_{\mathrm{centripete}} = mr\dot{\theta}^2\vec{e_r} = \alpha \vec{e_r}[/TEX], vecteur dirigé selon [TEX]\vec{e_r}[/TEX], sortant par rapport au centre du mouvement.

Cela signifie que tout objet massique en mouvement circulaire uniforme est soumis à une force l'entraînant vers l'extérieur du centre du mouvement. Cette force est corrélée avec la masse de l'objet, la distance à laquelle il se trouve du centre de mvmt et varie comme le carré de sa vitesse angulaire : Plus l'essoreuse tourne vite, plus elle plaquera les feuilles de salade contre la paroi externe !

C'est aussi ce phénomène qui explique que les satellites en rotation autour de la Terre ne tombent pas : Ils sont soumis à une force d'inertie qui vient exactement contrer la force de gravitation.

Nota : J'ai ici considéré le mouvement d'un point massique. En réalité, on travaille dans le cadre de solides (systèmes constitués de plusieurs points massiques, qui ne peuvent pas se déformer). Seulement, les travaux en mécanique du solide montrent que l'accélération de l'objet est peu ou prou celle de son centre d'inertie, s'il ne tourne pas sur lui-même... Les résultats démontrés ici se généralisent donc aisément dans le cas des solides, et donc des laitues, satellites, pommes, etc.

II) Rotation fluide

a) Pré-requis

Un fluide, en mécanique des milieux continus, est un système de particules formant un système déformable.

En règle générale, un fluide obéit à des lois de comportement rhéologique (comportement visqueux) et à des lois de conservation. Nous pouvons synthétiser ces informations dans un système d'équations de conservation que l'on appelle les équations de Navier-Stokes (au cœur d'un défi mathématique d'envergure, actuellement) :

(1) : Conservation de la masse [TEX]\frac{\partial \rho}{\partial t} + \nabla\cdot{\rho \vec{U}} = 0[/TEX]

Il s'agit d'une évidence démographique :

Cette équation, issue d'un bilan intégral, dit que l'évolution de la masse d'un système est due à une masse entrante à laquelle on soustrait une masse sortante, à chaque instant. Pour une particule gardant ses éléments, au cours du temps, il est naturel que la masse de la particule se conserve, ce que l'on traduit dans cette équation par "la densité de la particule varie, selon le temps, comme le flux de densité qui la traverse".

(2) : Conservation de la quantité de mouvement

[TEX]\rho\frac{\mathrm{D}\vec{U}}{\mathrm{D}t} = -\nabla P + \vec{f} + \(\lambda_n + \mu_n\)\nabla\(\nabla\cdot \vec{U}\) + \mu_n\Delta \vec{U}[/TEX]

Il s'agit d'un analogue au principe fondamental de la dynamique, en mécanique du solide :

La quantité de mouvement d'une particule - sa masse à laquelle on multiplie sa vitesse - varie si on lui applique des forces. Dans l'ordre (dans le membre de droite), on peut voir la force volumique de pression, les forces volumiques autres (genre gravité, forces électromagnétiques, etc.) et deux termes de viscosité.

(3) Conservation de l'énergie interne du système

[TEX]\rho\frac{\mathrm{D}e}{\mathrm{D}t} = r + k\Delta T - p\nabla\cdot\vec{U} +\lambda_n\(\nabla\cdot \vec{U}\) ^2+ 2\mu_n\mathrm{D}:\mathrm{D}[/TEX] où [TEX]\mathrm{D}:\mathrm{D}[/TEX] est le produit doublement contracté de D par lui-même, alias la trace du tenseur D², avec D le tenseur des déformations du fluide.

Cette équation traduit le fait que l'énergie interne (notion introduite en thermodynamique) de la particule varie s'il y a création d'énergie au sein du système, s'il y a diffusion thermique à la surface de la particule, s'il y a un travail de compression de la particule et enfin, si les forces internes de viscosité dissipent de la chaleur.

Ce qu'il y a de notable, dans le cas des fluides incompressibles (ou en tout cas peu compressibles), c'est que leur comportement est régi par la seconde équation que l'on transforme en :

(2-bis) : Conservation de la quantité de mouvement, cas incompressible

[TEX]\rho_0\frac{\mathrm{D}\vec{U}}{\mathrm{D}t} = -\nabla P + \vec{f} + \mu_n\Delta \vec{U}[/TEX] avec [TEX]\rho = \rho_0 = constante[/TEX] puisque le fluide est incompressible.

La première équation, elle, se traduit par :

(1-bis) : Conservation de la masse, cas incompressible

[TEX]\nabla\cdot{\vec{U}} = 0[/TEX]

"La vitesse ne diverge pas : Son flux se conserve le long d'un tube de courant". Autrement dit, il n'existe pas d'endroit dans l'espace où le champ de vitesse pourrait faire gonfler ou comprimer la matière. L'écoulement est isochore, à densité constante.

b) Hypothèses

Ce sujet est en construction.

Il vous semble sans doute horrible, à première vue. Ne vous inquiétez pas, je veillerai à ce qu'il soit lisible. Les démonstrations mathématiques sont laissées pour moi-même (afin que je sache où aller) et d'éventuels connaisseurs